.Ein neuronales Netz mit Radialen Basisfunktionen (RBF) besteht aus einer Eingangschicht, einer inneren Schicht und einer Ausgabeschicht. Die Ausgabe berechnet sich aus einer Linearkombination der lokalen Basisfunktionen der l1 inneren Knoten und einer anschließenden nicht linearen Transformation .
Als Radiale Basisfunktion wird meist die mehrdimensionale Gaußfunktion verwendet.
 |
 |
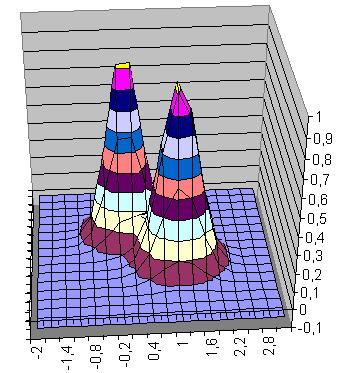
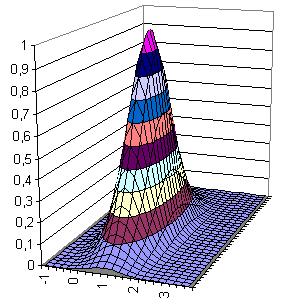Abbildung 1 Basisfunktion  mit Zentrum c=3
|
Abbildung 2 Basisfunktion  mit Zentrum  und Sigma 
|
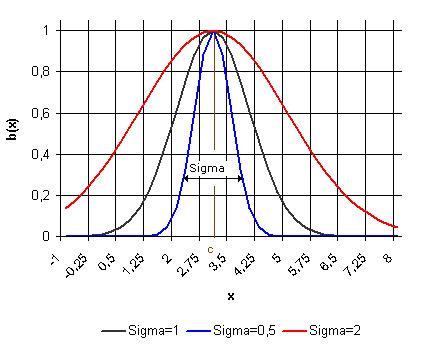
Die Basisfunktionen besitzen im allgemeinen zwei Parameter, das Zentrum 
und die Weite 
. Die Basisfunktionen sind lokal, den nur wenn die Eingabe 
nahe am Zentrum 
liegt, trägt die Basisfunktion etwas zur Ausgabe bei.
Als weiteren Parameter habe ich einen Faktor 
mit aufgenommen, der direkten mit der Eingabe gekoppelt ist. Werden die Netzparameter mit einem Gradientenabstiegsverfahren erlernt, kann dies auch auf 
angewendet werden. Ein spezieller Term in der Fehlerfunktion bewirkt, das das Lernverfahren kleine 
bevorzugt. Ist ein 
, kann der Eingangskonten 
nach dem Lernen entfernt werden, da dieser nichts zur Ausgabe beiträgt. Die Netztopologie (der Eingangskonten) wird mittels 
mit erlernt. Initialisiert (vorm dem Lernvorgang) wird mit 1.
Setzt man (1) und (2) in (3) erhält man
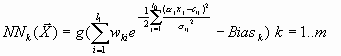
Werden die Parameter 
durch ein Iteratives Lernverfahren bestimmt, wird meist die Fehlerfunktion
verwendet.
Die Terme 
und 
werden verwendet um die Parameter 
und 
klein zu halten.
Die freien Parameter können über ein Gradientenabstiegsverfahren bestimmt werden. Die Deltas müssen dabei nicht wie bei MLP-Netzwerken zurückprobagiert werden. Es reicht wenn für jeden Parameter das Gradientenverfahren angewendet wird.
Berechnung der Gradienten
Folgende Ableitung werden später benötigt:
, 
, 
, 
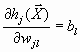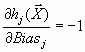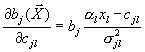
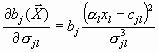Gradient für (Differenzieren von (4) nach )
Gradient für (Differenzieren von (4) nach )
Gradient für
Gradient für
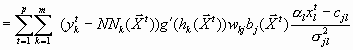
Gradient für
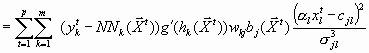
Berechnung der neuen Parameterwerte im Iterationsschritt
:
wobei
die Lernraten der Parameter sind.
Initialisierung der Parameter
=1, zufällige Initialisierung,, zufällige Initialisierung oder über ein Clusterverfahren (z.B. K-Means-Clustering)
, Einheitliche Werte. Wenn für die Zentren ein Clusterungsverfahren verwendet wurde 
, wobei 
der maximale Abstand der Cluster und 
die Anzahl der Cluster ist.
Sensitivität des trainierten Netzes
Die Sensitivität des Netzes auf die Eingangvariablen kann mittels der Jakobian Matrix untersuchen
werden. Die Elemente der Jakobian Matrix sind die Ersten Ableitung der Netzwerkfunktion (2) nach den Eingangsvariablen.
.
Beispiel
XOR